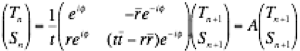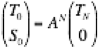C.G.Darwinは、結晶をその表面に平行な原子層の積み重ねとみなして、それらの原子層による多重散乱の総和をとることによって、X線の回折を説明しました。我々の研究室では、Bragg条件が満たされないときにもDarwin流の考えが適用できるようにその理論を拡張して、CTR散乱と呼ばれている散乱を説明することに成功しました。
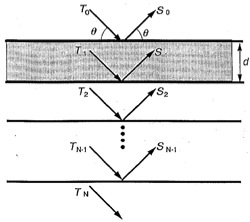
各々の原子層の直上で入射波の方向に進むX線の波をT、反射波の方向に進む波をSとすると、隣接した原子層でのTn,Tn+1及びSn,Sn+1 の間の関係は下図のようになります。ここでtとrは原子層でのX線の透過率と反射率で、-(バー)がついているものは原子層の裏面に関するそれらの量です。またφは隣接する原子層間で生じるX線の位相差です。
図の関係式を厳密に解いて、X線の反射率を計算しました。
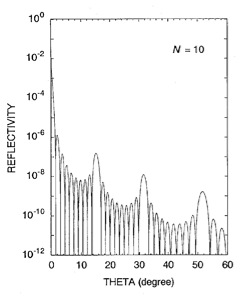
例として、シリコンの(001)面にモリブデンのKα線を入射させた場合の反射率を視射角の関数として計算した図を示します。第一の図は原子層が10枚という極めて薄い結晶について計算したもので、その結果はLaue関数とほぼ同じになります。
第二の図は、原子層が100枚のものです。副極大がつながって懸垂線のような形ができています。
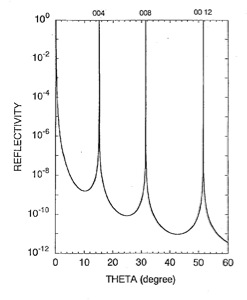
最後の図は原子層数を無限大にしたもので、現実の結晶はこれに相当します。通常の運動学的な取り扱いでは、Braggピークで反射強度が無限大に発散してしまうのですが、我々の結果では、正しく反射率が1になっています。またBraggピークの間にも有限の強度の散乱が存在していることがわかります。この散乱がCTRと呼ばれるものです。
Surf. Sci. 311 (1994) 433-439.
Surf. Sci. 326 (1995) 347-360.